Evaluate the series or state that it diverges – Evaluating whether a series converges or diverges is a fundamental concept in mathematics. By understanding the techniques and tests involved, we gain insights into the behavior of infinite series, enabling us to determine their limits and identify patterns.
This guide provides a comprehensive overview of series convergence and divergence, covering various tests and special series to equip you with the necessary knowledge for effective evaluation.
Evaluate Convergence/Divergence

To evaluate whether a series converges or diverges, we can use various tests. A series converges if its sequence of partial sums approaches a finite limit, and diverges if it does not. Some common tests for convergence include the ratio test, root test, and comparison test.
Ratio Test
- If the limit of the absolute value of the ratio of consecutive terms is less than 1, the series converges absolutely.
- If the limit of the absolute value of the ratio of consecutive terms is greater than 1, the series diverges.
- If the limit of the absolute value of the ratio of consecutive terms is equal to 1, the ratio test is inconclusive.
Root Test
- If the limit of the nth root of the absolute value of the nth term is less than 1, the series converges absolutely.
- If the limit of the nth root of the absolute value of the nth term is greater than 1, the series diverges.
- If the limit of the nth root of the absolute value of the nth term is equal to 1, the root test is inconclusive.
Comparison Test
- If the terms of a series are less than or equal to the terms of a convergent series, then the given series converges.
- If the terms of a series are greater than or equal to the terms of a divergent series, then the given series diverges.
Convergence Tests: Evaluate The Series Or State That It Diverges
Ratio Test
The ratio test is a convergence test that compares the absolute values of consecutive terms in a series. If the limit of the ratio is less than 1, the series converges absolutely. If the limit of the ratio is greater than 1, the series diverges.
If the limit of the ratio is equal to 1, the ratio test is inconclusive.
Example, Evaluate the series or state that it diverges
Consider the series \(\sum_n=1^\infty \fracn2^n\). Using the ratio test, we have:
$$\lim_n\to\infty \left|\fraca_n+1a_n\right| = \lim_n\to\infty \left|\frac\fracn+12^n+1\fracn2^n\right| = \lim_n\to\infty \left|\fracn+12\cdot\frac2^nn\right| = \lim_n\to\infty \left|\frac2^n+22n\right| = \lim_n\to\infty \left(\frac12+\frac1n\right) = \frac12$$
Since the limit is less than 1, the series converges absolutely.
Root Test
The root test is a convergence test that compares the nth root of the absolute value of the nth term in a series. If the limit of the nth root is less than 1, the series converges absolutely. If the limit of the nth root is greater than 1, the series diverges.
If the limit of the nth root is equal to 1, the root test is inconclusive.
Example, Evaluate the series or state that it diverges
Consider the series \(\sum_n=1^\infty \fracn^2e^n\). Using the root test, we have:
$$\lim_n\to\infty \sqrt[n]\left|\fracn^2e^n\right| = \lim_n\to\infty \sqrt[n]\fracn^2e^n = \lim_n\to\infty \fracn^2/ne^n/n = \lim_n\to\infty \fracne^n = 0$$
Since the limit is less than 1, the series converges absolutely.
Comparison Test
The comparison test is a convergence test that compares the terms of a series to the terms of a convergent or divergent series. If the terms of a series are less than or equal to the terms of a convergent series, then the given series converges.
If the terms of a series are greater than or equal to the terms of a divergent series, then the given series diverges.
Example, Evaluate the series or state that it diverges
Consider the series \(\sum_n=1^\infty \frac1n^2+1\). Since the terms of this series are less than or equal to the terms of the convergent series \(\sum_n=1^\infty \frac1n^2\), the given series converges.
Divergence Tests

Divergence Test
The divergence test, also known as the nth term test for divergence, states that if the limit of the nth term of a series is not equal to 0, then the series diverges.
Example, Evaluate the series or state that it diverges
Consider the series \(\sum_n=1^\infty \fracnn+1\). The limit of the nth term is:
$$\lim_n\to\infty \fracnn+1 = 1 \neq 0$$
Since the limit is not equal to 0, the series diverges.
Special Series
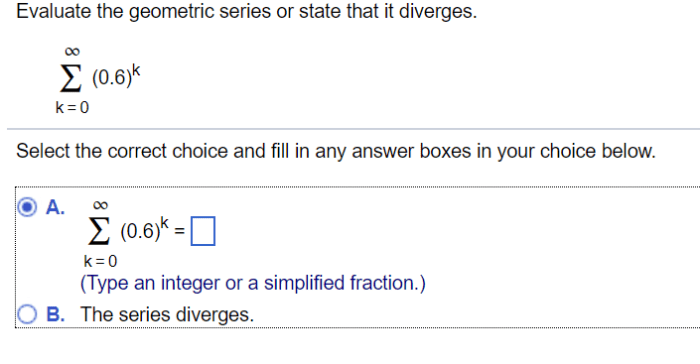
Geometric Series
A geometric series is a series of the form \(\sum_n=0^\infty ar^n\), where ais the first term and ris the common ratio. A geometric series converges if and only if |r| < 1. If |r| < 1, the sum of the series is \(\fraca1-r\).
Telescoping Series
A telescoping series is a series of the form \(\sum_n=1^\infty (a_n- a_n+1)\) . A telescoping series converges if and only if the limit of a_nas napproaches infinity exists. If the limit of a_nas napproaches infinity exists, the sum of the series is \(a_1- \lim_n\to\infty a_n\) .
Example, Evaluate the series or state that it diverges
Consider the telescoping series \(\sum_n=1^\infty \left(\frac1n- \frac1n+1\right)\) . The limit of a_nas napproaches infinity is 0, so the sum of the series is \(1- 0 = 1\) .
Questions Often Asked
What is the ratio test?
The ratio test is a convergence test that examines the limit of the absolute value of the ratio of consecutive terms in a series. If the limit is less than 1, the series converges absolutely; if it is greater than 1, the series diverges; and if it is equal to 1, the test is inconclusive.
How do I use the comparison test to evaluate convergence?
The comparison test compares a given series to a known convergent or divergent series. If the terms of the given series are less than or equal to the terms of the convergent series, then the given series also converges. Conversely, if the terms of the given series are greater than or equal to the terms of the divergent series, then the given series also diverges.