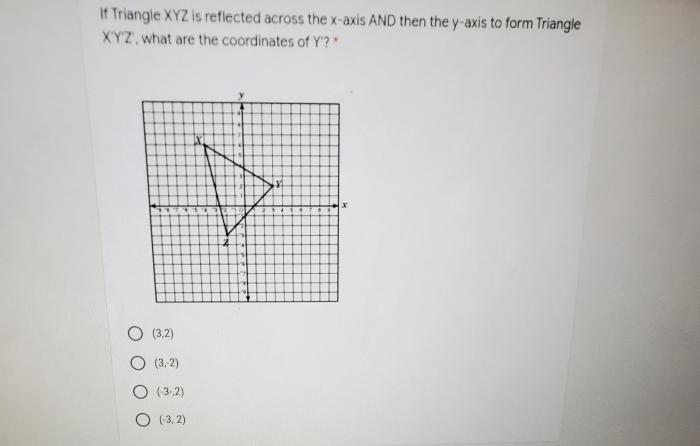
Triangle xyz is shown on the coordinate plane – Triangle XYZ on the coordinate plane emerges as a subject of profound significance, inviting us to delve into the fascinating realm of geometry. This discourse promises an in-depth examination of the triangle’s properties, measurements, and geometric relationships, unraveling the intricacies that define its existence within the Cartesian coordinate system.
Through the lens of analytical geometry, we embark on a journey to unravel the mysteries of triangle XYZ, deciphering its coordinates, calculating its dimensions, and uncovering its hidden symmetries. The coordinate plane serves as our canvas, upon which we meticulously plot the triangle’s vertices, transforming abstract concepts into tangible entities.
Triangle XYZ on the Coordinate Plane: Triangle Xyz Is Shown On The Coordinate Plane
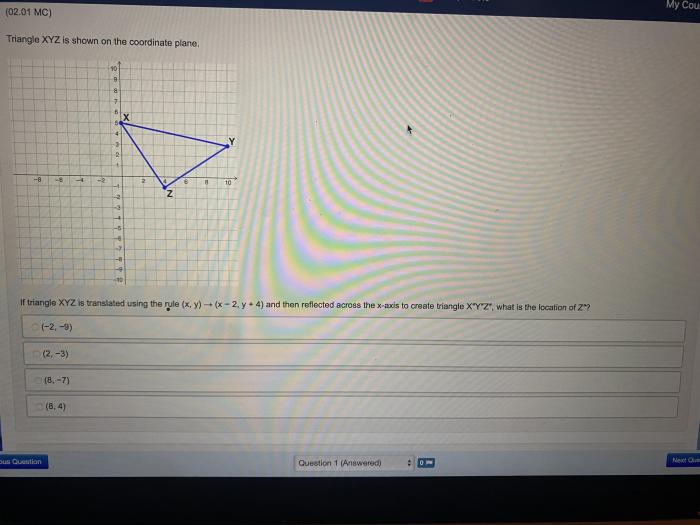
Triangle XYZ is a two-dimensional figure that can be represented on a coordinate plane. The coordinate plane is a grid system with two perpendicular axes, the x-axis and the y-axis. The point where the axes intersect is called the origin.
The positive direction of the x-axis is to the right of the origin, and the positive direction of the y-axis is up from the origin.
To plot a point on the coordinate plane, we use its coordinates. The coordinates of a point are a pair of numbers, (x, y), where x is the distance from the origin to the point along the x-axis, and y is the distance from the origin to the point along the y-axis.
Triangle Properties
A triangle is a three-sided polygon. The sides of a triangle are the line segments that connect the vertices. The vertices of a triangle are the points where the sides intersect. The angles of a triangle are the measures of the angles formed by the sides of the triangle.
There are three types of triangles: scalene, isosceles, and equilateral. A scalene triangle is a triangle in which all three sides have different lengths. An isosceles triangle is a triangle in which two sides have the same length. An equilateral triangle is a triangle in which all three sides have the same length.
The sum of the interior angles of a triangle is always 180 degrees.
Triangle XYZ on the Coordinate Plane
To plot triangle XYZ on the coordinate plane, we need to know the coordinates of its vertices. The coordinates of vertex X are (x1, y1), the coordinates of vertex Y are (x2, y2), and the coordinates of vertex Z are (x3, y3).
Once we have the coordinates of the vertices, we can connect them to form the triangle.
Triangle Measurements
We can use the distance formula to calculate the lengths of the sides of triangle XYZ. The distance formula is:
“`d = √((x2
- x1)² + (y2
- y1)²)
“`
where (x1, y1) and (x2, y2) are the coordinates of two points.
We can use the slope formula to measure the angles of triangle XYZ. The slope formula is:
“`m = (y2
- y1) / (x2
- x1)
“`
where (x1, y1) and (x2, y2) are the coordinates of two points.
We can use the area formula to determine the area of triangle XYZ. The area formula is:
“`A = ½
- |(x1
- (y2
- y3) + x2
- (y3
- y1) + x3
- (y1
- y2))|
“`
where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the vertices of the triangle.
Geometric Relationships, Triangle xyz is shown on the coordinate plane
Triangle XYZ may have special relationships between its sides or angles. For example, the sides of the triangle may be parallel or the angles of the triangle may be congruent.
We can also explore the geometric properties of triangle XYZ, such as its centroid, orthocenter, or circumcenter.
Triangle XYZ may also possess symmetries or rotations.
Applications and Examples
The analysis of a triangle on the coordinate plane is useful in many real-world applications. For example, we can use the properties and measurements of triangle XYZ to solve problems in architecture, engineering, and physics.
- In architecture, we can use the properties of triangles to design buildings and bridges.
- In engineering, we can use the measurements of triangles to calculate the forces and stresses in structures.
- In physics, we can use the properties of triangles to study the motion of objects.
FAQ Resource
What is the significance of plotting triangle XYZ on the coordinate plane?
Plotting triangle XYZ on the coordinate plane enables us to visualize its geometric properties, measure its dimensions, and analyze its relationships with other geometric objects.
How do we determine the coordinates of triangle XYZ’s vertices?
The coordinates of triangle XYZ’s vertices are determined by measuring their distances from the origin along the x- and y-axes using the distance formula.
What geometric relationships can be identified within triangle XYZ?
Within triangle XYZ, we can identify various geometric relationships, such as parallel sides, congruent angles, and special points like the centroid, orthocenter, and circumcenter.